问题
问答题
求微分方程y"-2y’-3y=3x+1+e-x+sin2x的通解．
答案
参考答案：将方程右端作变形，得
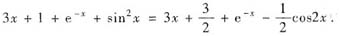
(1)特征方程λ2-2λ-3=0，特征根λ1=-1，λ2=3，则相应齐次微分方程通解
(2)求原方程一个特解y*．因为
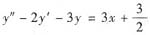有特解
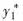=ax+b；y"-2y’-3y=e-x有特解
有特解
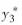=dcos2x+esin2x，所以
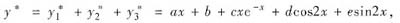
其中a，b，c，d，e为待定系数．将y*代入原方程得待定系数
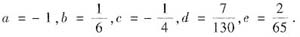
于是
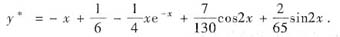
(3)原方程通解为
