问题
问答题
求微分方程y"+4y=3|sinx|在[-π,π]上满足
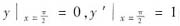 的特解.
的特解.
答案
参考答案:当-π≤x≤0时,方程为y"+4y=-3sinx,可求得该方程的通解为
y=C1cos2x+C2sin2x-sinx.
当0<x≤1T时,方程为y"+4y=3sinx,可求得此方程的通解为
y=C3cos2x+C4sin2x+sinx.
由于方程的解y(x)及其导函数y’(x)都在分段点x=0处连续,所以
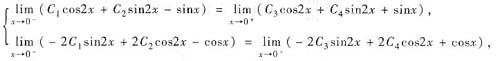
从而C1=C3,C2=C4+1.
故原方程通解为

又因为

因此所求特解为

