问题
问答题
设
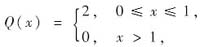 求微分方程
求微分方程
 =Q(x)(x∈[0,+∞),x≠1)满足初始条件y(0)=0的连续解.
=Q(x)(x∈[0,+∞),x≠1)满足初始条件y(0)=0的连续解.
答案
参考答案:当0≤x≤1时,微分方程为
 ,这是一阶线性微分方程,通解为y=C1e-x+2;
,这是一阶线性微分方程,通解为y=C1e-x+2;
当x>1时,微分方程为
 ,这是变量可分离的微分方程,通解为y=C2e-x.
,这是变量可分离的微分方程,通解为y=C2e-x.
根据y(x)的连续性知:
 ,所以C2=C1+2e.
,所以C2=C1+2e.
故原方程的通解为

由于y(0)=0,所以C=-2,故满足条件的特解为

设
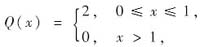 求微分方程
求微分方程
 =Q(x)(x∈[0,+∞),x≠1)满足初始条件y(0)=0的连续解.
=Q(x)(x∈[0,+∞),x≠1)满足初始条件y(0)=0的连续解.
参考答案:当0≤x≤1时,微分方程为
 ,这是一阶线性微分方程,通解为y=C1e-x+2;
,这是一阶线性微分方程,通解为y=C1e-x+2;
当x>1时,微分方程为
 ,这是变量可分离的微分方程,通解为y=C2e-x.
,这是变量可分离的微分方程,通解为y=C2e-x.
根据y(x)的连续性知:
 ,所以C2=C1+2e.
,所以C2=C1+2e.
故原方程的通解为

由于y(0)=0,所以C=-2,故满足条件的特解为
