问题
单项选择题
微分方程y"+2y’+y=(x+1)e-x+2x+1有一个特解y*形式为
(A) y*=x(ax+b)e-x+(cx+d)． (B) y*=(ax+b)e-x+x2(cx+d)．
(C) y*=x2(ax+b)e-x+(cx+d)． (D) y*=(ax+b)e-x+x(cx+d)．
答案
参考答案：C
解析： 因为特征方程为λ2+2λ+1=0，特征根为重根λ1=λ2=-1，所以对应于非齐次项(x+1)e-x应设特解
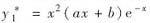，对应非齐次项2x+1应设特解
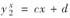，再由迭加原理知应设特解
y*=x2(ax+b)e-x+(cx+d)，
故应选(C)．