设
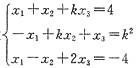 ,问方程组什么时候有解什么时候无解有解时,求出其相应的解.
,问方程组什么时候有解什么时候无解有解时,求出其相应的解.
参考答案:
 .
.
当|A|=(1+k)(4-k)≠0即k≠-1,4时,r(
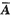 )=r(A)=3,方程组有唯一解,且由克拉默法则易求得唯一解为
)=r(A)=3,方程组有唯一解,且由克拉默法则易求得唯一解为
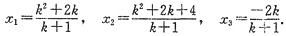
当k=-1时,方程组为
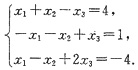
此时,
 .
.
因r(A)=2<r(
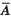 )=3,故方程组无解.
)=3,故方程组无解.
当k=4时,方程组为
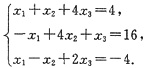

因r(
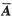 )=r(A)=2<n=3,故方程组有解,且有无穷多解
)=r(A)=2<n=3,故方程组有解,且有无穷多解
由基础解系和特解的简便求法即得基础解系为α=[-3,-1,1]T,特解为η=[0,4,0]T,故所求通解为
η+kα=[0,4,0]T+k[-3,-1,1]T,k为任意常数.
解析: 使用初等行变换将其增广矩阵化为行阶梯形矩阵,分别讨论k取何值时,r(
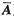 )≠r(A),r(
)≠r(A),r(
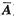 )=r(A)=3,r(
)=r(A)=3,r(
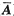 )=r(A)<3.有解时,再求其解.
)=r(A)<3.有解时,再求其解.

