问题
问答题
设二次型
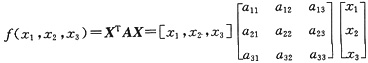
满足
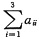 =2,AB=O,其中
=2,AB=O,其中
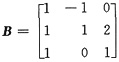 .
.
用正交变换化二次型为标准形,并求所作的正交变换
答案
参考答案:由AB=O即知B中三个列向量均为A的属于零特征值的特征向量.
事实上,设B=[α1,α2,α3],则Aαi=0(i=1,2,3).显然α1,α2线性无关,且α3-α1+α2,故λ1=0至少是二重特征值.又因
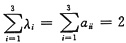
故λ1=λ2=0,λ3=2.设对应于λ3=2的特征向量为
β3=[x1,x2,x3]T,则α1与β3,α2与β3正交,于是有
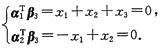
由
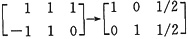 知,该方程组的基础解系为
知,该方程组的基础解系为
[-1/2,-1/2,1]T
为方便计,取β3=[1,1,-2]T.
注意到α1,α2,α3两两正交,只需单位化
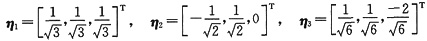 ,
,
则Q=[η1,η2,η3]为正交矩阵,作正交变换X=QY,则
f=XTAX=(QY)TA(QT)=YT(QTAQ)y
=

