问题
单项选择题
设X1,X2,…,Xn,…是相互独立的随机变量序列,Xn服从参数为n(n=1,2,…)的指数分布,则下列不服从切比雪夫大数定律的随机变量序列是______.
A.X1,X2,…,Xn,…
B.X1,22X2,…,n2Xn,…
C.X1,X2/2,…,Xn/n,…
D.X1,2X2,…,nXn,…
答案
参考答案:B
解析: 根据切比雪夫大数定律所要求的条件判别.
切比雪夫大数定律要求三个条件:首先是要求X1,X2,…,Xn相互独立;其次是要求Xn(n=1,2,…)的期望和方差都存在;最后还要求方差一致有界,即对任何正整数n,D(Xn)<L,其中L是与n无关的一个常数.
题中四个随机变量序列显然全满足前两个条件,由于
对于A,有
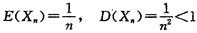 ;
;
对于B,有

对于C,有
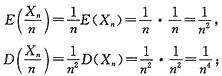
对于D,有
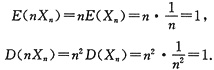
显然B序列的方差D(n2Xn)不能对所有n均小于一个共同常数,因此不满足切比雪夫大数定律.
综上分析,仅B入选.
