问题
问答题
设钢管内径X服从正态分布N(μ,σ2),规定内径在98到102之间的为合格品;超过102的为废品,不是98的为次品.已知该批产品的次品率为15.9%,内径超过101的产品在总产品中占2.28%,求整批产品的合格率.
答案
参考答案:要求产品合格率,即要计算P(98≤X≤102),而计算正态分布随机变量取值的概率,需要已知分布参数μ与σ2.为此,应先根据条件确定μ与σ2的值.
依题意知
P(X<98)=0.159,P(X>101)=0.0228,
0.159=P(X<98)=P(X≤98)=
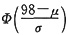 ,
,
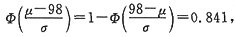 ①
①
0.0228=P(X>101)=1-P(X≤101)=
 ,
,
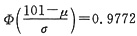 ②
②
根据式①与式②,查正态分布表可得关于μ与σ的二元方程组:
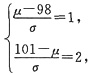 解得
解得

于是P(98≤X≤102)=Φ(102-99)-Φ(98-99)
=Φ(3)-Φ(-1)=0.83995.
解析: 求正态分布随机变量满足一定条件的概率,一般都应先标准化.利用标准正态分布求概率或建立未知参数的函数关系,这是常用的方法与技巧.要计算P(98≤X≤102),必标准化,要标准化必须知道参数μ和σ2.为此,先利用题设条件求出μ与σ2的值.
