参考答案：齐次方程y"-3y’-4y=0的特征方程为
λ²-3λ-4=0，
由此求得特征根λ₁=4，λ₂=-1．对应齐次方程的通解为
Y=C₁e^4x+C₂e^-x．
则f₁(x)=(10x-7)e^-x的特解形式为

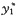=x(A+Bx)e^-x=(Ax+Bx²)e^-x，
f₂(x)=34sinx的特解形式为

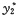=Csinx+Dcosx．
于是由叠加原理知，非齐次方程的特解为

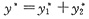=(Ax+Bx²)e^-x+Csinx+Dcosx，
则(y^*)’=(A+2Bx-Ax-Bx²)e^-x+Ccosx-Dsinx，
(y^*)"=(2B-2A-4Bx+Ax+Bx²)e^-x-Ccosx-Dsinx，
代入原方程，求得A=1，B=-1，C=-5，D=3，从而
y^*=x(1-x)e^-x-5sinx+3cosx．
于是原方程的通解为
y=y+y^*=C₁A^4x+(C₂+x-x²)e^-x-5sinx+3cosx．

解析： 利用二阶非齐次线性方程解的叠加原理求之．
设

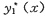与

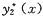分别是方程
y"+p(x)y’+q(x)y=f₁(x)
与y"+p(x)y’+q(x)y=f₂(x)的特解，则
y^*(x)=

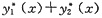是方程
y"+p(x)y’+q(x)y=f₁(x)+f₂(x)的特解．