参考答案：A

解析： 由所给的二次积分易求出其积分区域如下图所示．由于积分区域为圆域的一部分，且被积函数又为f(x²+y²)，应使用极坐标求此二重积分．

所给曲线为(y+1)²+x²=1的上半圆周，区域D如上图所示，其直角坐标方程为
(y+1)²+x²≤1，即y²+x²≤-2y，
将x=rcosθ，y=rsinθ代入得到极坐标系下的方程
r²≤-2rsinθ，即r≤-2sinθ．
于是D={(r，θ)|-π/4≤θ≤0，0≤r≤-2sinθ}，
则

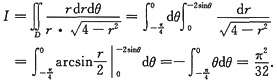
仅A入选．