问题
单项选择题
设A是四阶方阵,A*是A的伴随矩阵,其特征值为1,-1,2,4,则下列矩阵中为可逆矩阵的是______.
A.A-E
B.2A-E
C.A+2E
D.A-4E
答案
参考答案:A
解析: 利用矩阵行列式与其矩阵特征值的关系:|A|=λ1λ2…λn判别之,其中λi为A的特征值.
解一 设A*的特征值为
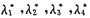 ,则
,则
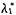 =1,
=1,
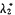 =-1,
=-1,
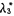 =2,
=2,
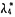 =4,
=4,
于是|A*|=1·(-1)·2·4=-8.
因而|A|4-1=|A*|,故|A|3=-8,即|A|=-2,所以A的特征值为

因而A-E的特征值为
μ1=-2-1=-3,μ2=2-1=1
μ3=-1-1=-2,μ4=-1/2-1=-3/2,
故|A-E|=μ1·μ2·μ3·μ4=-9≠0,所以A~E可逆.
解二 由A的特征值易求得其他矩阵2A-E,A+2E,A-4E的特征值分别都含有零特征值,因而其行列式等于0,它们均不可逆.仅A入选。
