解：（1）a₂=a₁+（-1）¹=0，

a₃=a₂+3¹=3

a₄=a₃+（-1）²=4，

a₅=a₄+3²=13，

所以，a₃=3，a₅=13。

（2）a_2k+1=a_2k+3^k =a_2k-1+（-1）^k+3^k，

所以a_2k+1-a_2k-1=3^k+（-1）^k，

同理a_2k-1-a_2k-3=3^k-1+（-1）^k-1，

……

a₃-a₁=3+（-1）

所以（a_2k+1-a_2k-1）+（a_2k-1-a_2k-3）+…+（a₃-a₁）

=（3^k+3^k-1+…+3）+[（-1）^k+（-1）^k-1+…+（-1）]，

由此得a_2k+1-a₁=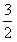（3^k-1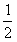）+[（-1）^k-1]，

于是a_2k+1=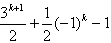

a_2k=a_2k-1+（-1）^k=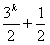（-1）^k-1-1+（-1）^k=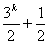（-1）^k=1

{a_n}的通项公式为：

当n为奇数时，a_n=；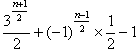

当n为偶数时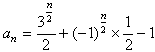，。