问题
解答题
在数列{an}中，a1=1，an+1=can+cn+1（2n+1）(n∈N*），其中实数c≠0。
（1）求{an}的通项公式；
（2）若对一切k∈N*有a2k>a2k-1，求c的取值范围。
答案
解：（1）由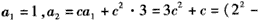
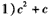
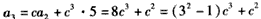
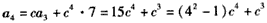
猜测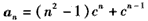
，n∈N*
下用数学归纳法证明
当n=1时，等式成立；
假设当n=k时，等式成立，
即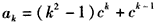
则当n=k+1时
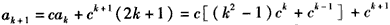
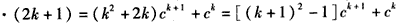
综上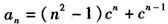
，对任何n∈N*都成立；
（2）由a2k>a2k-1，得
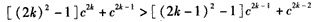
因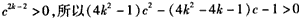
解此不等式得：对一切k∈N*，有c>ck或c＜ck′
其中ck=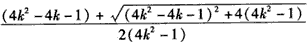
易知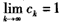
又由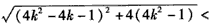
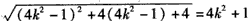
知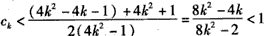
因此由c>ck对一切k∈N*成立得c≥1
又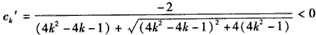
易知ck'单调递增，故ck'≥c1'对一切k∈N*成立，因此由c<ck'对一切k∈N*成立得
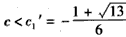
从而c的取值范围为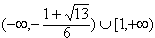
。