问题
解答题
设a1=2，a2=4，数列{bn}满足bn=an+1-an，bn+1=2bn+2，求数列{an}的通项公式。
答案
解：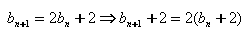
，
∵
，
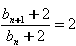又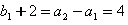
，
∴数列{bn+2}是首项为4，公比为2的等比数列，
∴
，
∴
，
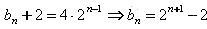令n=1，2，…（n-1），叠加得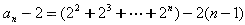
，
∴
。
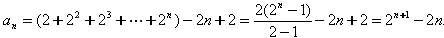搜题请搜索小程序“爱下问搜题”
设a1=2，a2=4，数列{bn}满足bn=an+1-an，bn+1=2bn+2，求数列{an}的通项公式。
解：，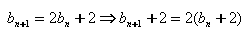
∵，
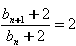又，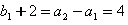
∴数列{bn+2}是首项为4，公比为2的等比数列，
∴，
∴，
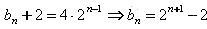令n=1，2，…（n-1），叠加得，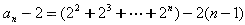
∴。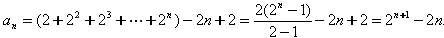