若矩阵A=
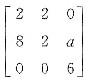 相似于对角矩阵A,试确定常数a的值;并求可逆矩阵P使P-1AP=A.
相似于对角矩阵A,试确定常数a的值;并求可逆矩阵P使P-1AP=A.
参考答案:由题设,先求矩阵A的特征值,设E为3阶单位矩阵,则由

可得λ1=6,λ2=6,λ3=-2.欲使A相似于对角阵Λ,应使λ1=λ2=6对应两个线性无关的特征向量,因此A-6E的秩为1,于是

可得出a=0,从而

下面求特征向量:
当λ1=λ2=6时,由(A-6E)x=0,可得出两个线性无关的特征向量为:
ξ1=(0,0,1)T, ξ2=(1,2,0)T.
当λ3=-2时,由(A+2E)x=0,可得
ξ3=(1,-2,0)T.
于是

且P-1存在,并有P-1AP=A,其中:

解析:[考点提示] 相似矩阵、对角化.
