问题
填空题
设3阶方阵A,B满足A2B-A-B=E,其中E为3阶单位矩阵,若A=
 则|B|=______.
则|B|=______.
答案
参考答案:
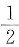
解析:[考点提示] 行列式、矩阵方程.
[解题分析] 由题设所给方程A2B-A-B=E,得
(A2-E)B=A+E,
即 (A+E)(A-E)B=A+E.
又由已知
[*]
则
[*]
且 |A+E|=3·(4+2)=18≠0.
又A-E=[*]且|A-E|+2≠0,于是
B=(A-E)-1(A+E)-1(A+E)=(A-E)-1.
因此|B|=[*]
