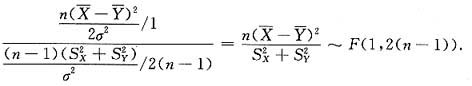问题
填空题
已知总体X与Y都服从正态分布N(0,σ2),X1,…,Xn与Y1,…,Yn为分别来自总体X与Y的两个相互独立的简单随机样本,样本均值与方差分别为
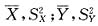 ,则统计量
,则统计量
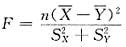 服从______分布,参数为______.
服从______分布,参数为______.
答案
参考答案:F;(1,2n-2)
解析: 由于两个总体都服从正态分布N(0,σ2),且样本又相互独立,因此容易求得

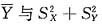 分布,再应用典型模式确定F的分布.
分布,再应用典型模式确定F的分布.
由于X~N(0,σ2),Y~N(0,σ2),所以
 相互独立,故
相互独立,故
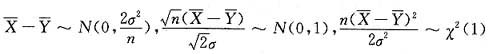 .
.
又
 相互独立,根据χ2分布可加性,得
相互独立,根据χ2分布可加性,得

又
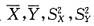 相互独立,从而推出
相互独立,从而推出
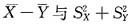 相互独立,由F分布的典型模式,得
相互独立,由F分布的典型模式,得