问题
填空题
设X1，X2…，X2n是来自正态总体N(μ，σ2)的简单随机样本(n≥2)，记样本均值
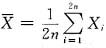，则统计量
(Xi+Xn+i-2
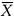)2的方差D(Y)=______．
答案
参考答案：8(n-1)σ4
解析： 构造新的简单随机样本：
X1+Xn+1，X2+Xn+2，…，Xn+X2n，显然Xi+Xn+i～N(2μ，2σ2)．
新样本均值和新样本方差为
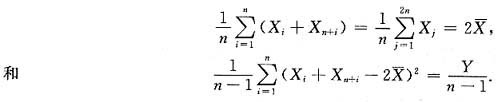
由性质
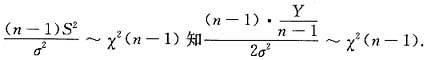
根据D(χ2(n-1))=2(n-1)得
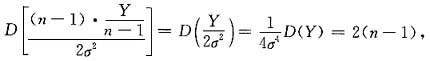
即D(Y)=8(n-1)σ4．