问题
填空题
设(X，Y)～N(μ1，μ2；
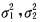；0)，其分布函数为F(x，y)，已知F(μ，y)=
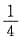，则y=______．
答案
参考答案：μ2．
解析： (X，Y)～N(μ1，μ2；
；0)，所以X，Y相互独立．
F(x，y)=FX(x)FY(y)，X～N(μ1，
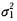)，Y～N(μ2，
)．
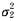由正态分布密度函数对称性，FX(μ1)=P{X≤μ}=
．
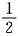F(μ1，y)=FX(μ1)FY(y)=
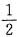FY(y)=
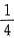，就有FY(y)=
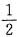，即y=μ2．