问题
问答题
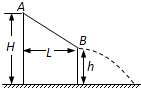
在一次消防逃生演练中,队员从倾斜直滑道AB的顶端A由静止滑下,经B点后水平滑出,最后落在水平地面的护垫上(不计护垫厚度的影响).已知A、B离水平地面的高度分别为H=6.2m、h=3.2m,A、B两点间的水平距离为L=4.0m,队员与滑道间的动摩擦因数μ=0.3,g取10m/s2.求:
(1)队员到达B点的速度大小;
(2)队员落地点到B点的水平距离;
(3)队员自顶端A至落地所用的时间.
答案
(1)设滑道的长度为LAB,倾角为θ,根据动能定理 有mg(H-h)-μmgLABcosθ=
mv021 2
v0=
=6m/s2g(H-h-μL)
队员到达B点的速度为6m/s;
(2)根据平抛运动的公式 有h=
g1 2
,x=v0t2t 22
得水平距离x=v0
=4.8m2h g
队员落地点到B点的水平距离为4.8m;
(3)设在滑道上运动的时间为t1,加速度为a,根据牛顿第二定律 有mgsinθ-μmgcosθ=ma
得a=gsinθ-μgcosθ=3.6m/s2
根据运动学公式 有LAB=
a1 2 t 21
h=
g1 2 t 22
得t1=
s=1.67s,t2=0.80s 5 3
运动的总时间t=t1+t2=2.47s
队员自顶端到地面所用的时间为2.47s.
