问题
填空题
已知随机变量X1与X2相互独立且分别服从参数为λ1，λ2的泊松分布，已知PX1+X2＞0=1-e-1，则E(X1+X2)2=______．
答案
参考答案：B
解析： 已知Xi～P(λi)且X1与X2相互独立，所以EXi=DXi=λi(i=1，2)，E(X1+X2)2=
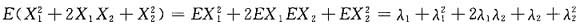=λ1+λ2+(λ1+λ2)2．为求得最终结果我们需要由已知条件计算出λ1+λ2．
因为P{X1+X2＞0)=1-P{X1+X2≤0}=1-P{X1+X2=0}
=1-P{X1=0，X2=0}=1-P{X1=0}P{X2=0}
=1-e-λ1·e-λ2-=1-e-(λ1+λ2)=1-e-1
所以λ1+λ2=1．故E(X1+X2)2=(λ1+λ2)+(λ1+λ2)2=2．