参考答案：0

解析： P{max(X，Y)＞μ)-P{min(X，Y)＜μ}
=1-P{max(X，Y)≤μ}-[1-P{min(x，y)≥μ}]
=-P{max(X，Y)≤μ}+P{min(X，Y)≥μ}
=-P{X≤μ，Y≤μ}+P{X≥μ，Y≥μ}
=-P{X≤μ}+P{X≤μ，Y＞μ}+P{X＞μ，Y＞μ}
=-P{X≤μ}+P{Y＞μ)=

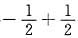=0．
记“X≤μ”=A，“Y≤μ”=B，显然P(A)”=P(B)=

．
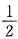P{max(X，Y)＞μ}-P{min(X，Y)＜μ}
=1-P{max(X，Y)≤μ)-[1-P{min(x，y)≥μ}]
=-P{max(X，Y)≤μ}+P{min(X，Y)≥μ}
=-P{X≤μ，Y≤μ}+P{X≥μ，Y≥μ}
=-P(AB)+P{X＞μ，Y＞μ}=-P(AB)+P

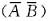
=-P(AB)+P

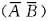=-P(AB)+1-P(A∪B)
=-P(AB)+1-P(A)-P(B)+P(AB)=1-P(A)-P(B)=1

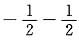=0．
本题中没有给出X，Y相互独立的条件，在上述计算中也没有用到相互独立的性质．不过在填空题计算中既然没说独立，显然对X，Y相互独立也是对的．不妨就用独立性质来计算，结果应该是一致的．
P{max(X，Y)＞μ}-P{min(X，Y)＜μ}
=1-P{max(X，Y)≤μ)-[1-P{min(x，y)≥μ}]
=-P{max(X，Y)≤μ}+P{min(X，Y)≥μ}
=-P{X≤μ，Y≤μ}+P{X≥μ，Y≥μ}
=-P{X≤μ}P{Y≤μ)+P{X≥μ}P{Y≥μ}
=

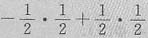=0