问题
填空题
已知
，又n维向量α1，α2，α3线性无关，则α1+α2，α2+2α3，Xα3+Yα1线性相关的概率为______．
答案
参考答案：
解析： 由于α1，α2，α3线性无关，所以“α1+α2，α2+2α3，Xα3+Yα1线性相关”
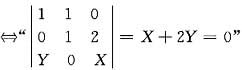，故所求的概率为
P{X+2Y=0}=P{X+2Y=0，Y=
}+P{X+2Y=0，Y≠
}
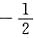=P{X=1，Y=
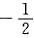}=P{X=1}=
．
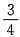(1)在解答概率论中与线性代数有关的问题时，我们总是先应用线性代数中的基本概念或充要条件，将所关心的事件表示出来，而后再应用概率论的方法去求解．
(2)如果P(A)=1，则对任意事件B都有P(AB)=P(B)即A与B独立．这是因为
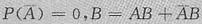，在本题计算过程中我们两次应用了这个结论．