问题
问答题
设二维随机变量X和Y的联合概率密度为
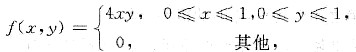
求X和Y的联合分布函数F(x.y).
答案
参考答案:如图所示,由[*]和F(x,y)=知当x<0或y<0时,F(x,y)=0;
当0≤x≤1,0≤y≤1时,
[*]
当x>1,0≤y≤1时,
[*]
[*]
当0≤x≤1,y>1时,
[*]
当x>1,y>1时,F(x,y)=1.
所以,X和Y的联合分布函数
[*]
解析:[考点提示] 由定义[*],因为f(x,y)是分段函数,要正确计算出F(x,y),必须根据f(x,y)的取值,对积分区域进行适当分块,即:x<0或y<0;0≤x≤1,0≤y≤1;x>1,0≤Y≤1;0≤x≤1,y>1及x>1,y>1等五个部分.
[评注] 求这类积分的原则是由积分区域S={(u,v)|u≤x,v≤y}与被积函数不为零的区域G={(u,v)1 0≤u,v≤1
