问题
问答题
假设f(x)在[a,+∞)上连续,f"(x)在(a,+∞)内存在且大于零,记
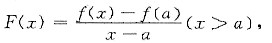
证明:F(x)在(a,+∞)内单调增加.
答案
参考答案:[详解1] [*]
令ψ(x)=f’(x)(x-a)-f’(x)+f(a)(x>a),
由于ψ’(x)=f’(x)(x=a)>0,
因此ψ(x)在(a,+∞)内单调增加,有ψ(x)>ψ(a)=0,
故[*]
所以F(x)单调增加.
[详解2] [*]
由中值定理知,存在ξ(a<ξ<x),使
[*]
于是,有
[*]
由于f"(x)>0,可见,f’(x)在(a,+∞)内单调增加.因此,对于任意x和ξ(a<ξ<x),有f’(x)>f’(ξ),从而F’(x)>0,于是F(x)是单调增加的.
解析:[考点提示] 要证F(x)在(a,+∞)内单调增加,只需证F’(x)>0,为此须先求出F(x)的导数F’(x),再利用f"(x)大于零的条件进行推证.
[评注] 一阶导数的符号可用来判定函数的单调性,但在求解具体问题时可能要通过多次求导才能最终得到一阶导数的符号.
