A市有某种型号的农用车50辆,B市有40辆,现要将这些农用车全部调往C、D两县,C县需要该种农用车42辆,D县需要48辆,从A市运往C、D两县农用车的费用分别为每辆300元和150元,从B市运往C、D两县农用车的费用分别为每辆200元和250元。
(1)设从A市运往C县的农用车为x辆,此次调运总费为y元,求y与x的函数关系式,并写出自变量x的取值范围;
(2)若此次调运的总费用不超过16000元,有哪几种调运方案?哪种方案的费用最小?并求出最小费用?
解:(1)从A市运往C县的农用车为x辆,此次调运总费为y元,根据题意得:
y=300x+200(42﹣x)+150(50﹣x)+250(x﹣2),
即y=200x+15400,
所以y与x的函数关系式为:y=200x+15400,
又∵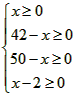 ,
,
解得:2≤x≤42,且x为整数,
所以自变量x的取值范围为:2≤x≤42,且x为整数;
(2)∵此次调运的总费用不超过16000元,
∴200x+15400≤16000
解得:x≤3,
∴x可以取:2或3,
方案一:从A市运往C县的农用车为2辆,从B市运往C县的农用车为40辆,从A市运往D县的农用车为48辆,从B市运往D县的农用车为0辆,
方案二:从A市运往C县的农用车为3辆,从B市运往C县的农用车为39辆,从A市运往D县的农用车为47辆,从B市运往D县的农用车为1辆,
∵y=200x+154000是一次函数,且k=200>0,y随x的增大而增大,
∴当x=2时,y最小,即方案一费用最小,
此时,y=200×2+15400=15800,
所以最小费用为:15800元。
