参考答案：(Ⅰ)α=(1，0，-2)^T是方程组(A^*-4E)x=0的一个解向量

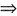(A^*-4E)-3α，所以α=(1，0，-2)^T是A的对应特征值λ₃=-3的特征向量；
设A的另外两个特征值为λ₁，λ₂则λ₁+λ₂+λ₃=1，λ₁λ₂λ₃=|A|=-12，解得λ₁=λ₂=2；
设λ₁=λ₂=2对应的特征向量为x=((x₁，x₂，x₃)^T，则它与α=(1，0，-2)^T正交，
即x₁-2x₃=0，其基础解系为α₁=(0，1，0)^T，α₂=(2，0，1)^T，
令P=(α₁，α₂，α)，则

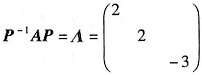，所以

。
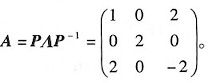(Ⅱ)(A^*+6E)x=0

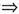(AA^*+6A)x=0

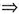(A-2E)x=0

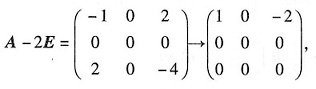
同解方程组为

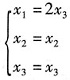，通解为k₁(0，1，0)^T+k²(2，0，1)^T，其中k¹，k²为任意常数。

解析：[考点] 矩阵的特征值，线性方程的解法