问题
问答题
设总体X～U(1，θ)，参数θ＞1未知，X1，…，Xn是来自X的简单随机样本。
(Ⅰ)求θ的矩估计和极大似然估计量；
(Ⅱ)求上述两个估计量的数学期望。
答案
参考答案：总体X～U(1，θ)，其分布密度为
(Ⅰ)由
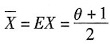，解得
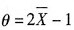，故θ的矩估计量为
；
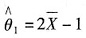似然函数
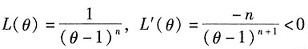，Lθ递减，
又X1，…，Xn∈(1，θ)，故θ的极大似然估计量为
。
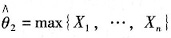(Ⅱ)
，
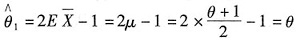而
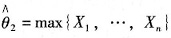的分布函数
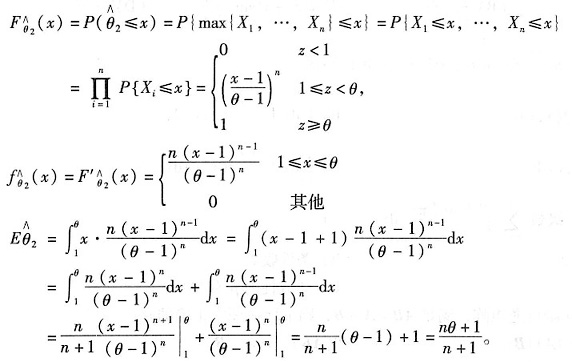
解析：[考点] 参数估计、期望