问题
问答题
设n阶实对称矩阵A的秩为r，且满足A2=A，求
(Ⅰ)二次型xTAx的标准形；
(Ⅱ)行列式|E+A+A2+…+An|的值，其中E为单位矩阵。
答案
参考答案：设Aα=λα(α≠0)，则A2α=λ2α，又，A2α=Aα=λα
故λ2α=λα
(λ2-λ)α=0
λ=1或者λ=0。
由n阶实对称矩阵A的秩为r知，λ=1，λ=0分别为A的r重和n-r重特征值，
故存在正交矩阵P，使得
。
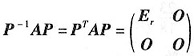(Ⅰ)经正交变换x=Py，二次型xTAx的标准形为
。
(Ⅱ)A2=A
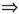A2=…=An=A，故行列式
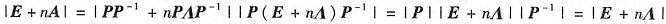=(n+1)r。
解析：[考点] 二次型的标准型、抽象行列式的计算