问题
问答题
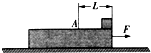
质量为m0的足够长的木板放在光滑水平地面上,在木板的上表面的右端放一质量为m的小金属块(可看成质点),如图所示,木板上表面的A点右侧是光滑的,A点到木板右端距离为L,A点左侧表面与金属块间的动摩擦因数为μ.现用一个大小为F的水平拉力向右拉木板,当小金属块到达A点时立即撤去此拉力.求:
(1)拉力F的作用时间是多少?
(2)最终木板的速度多大?
(3)小金属块到木板右端的最大距离为多少?
答案
(1)开始时,小金属块静止,对木板进行研究,根据牛顿第二定律:a=
…①F m0
设经时间t小金属块到达木板上表面的A点,则:L=
at2…②1 2
联立①②解得:t=
…③2m0L F
(2)当小金属块到达木板上表面的A点时,木板的速度为 v1=at=
…④,2FL m0
此后小金属块和木板相互摩擦直至速度相等的过程中,动量守恒:m0vl=(m0+m)v2 …⑤
联立④⑤解得,最终木板的速度为:v2=
…⑥2Fm0L m0+m
(3)小金属块和木板相互摩擦直至速度相等的过程能量守恒:μmgs=
m01 2
-v 21
(m0+m)1 2
…⑦v 22
联立④⑥⑦解得,小金属块和木板相互摩擦的距离s=
…⑧FL μg(m0+m)
小金属块到木板右端的最大距离 s总=s+L=
+L…⑨FL μg(m0+m)
答:(1)拉力F的作用时间是
.2m0L F
(2)最终木板的速度
.2Fm0L m0+m
(3)小金属块到木板右端的最大距离为
+L.FL μg(m0+m)
