问题
问答题
设f(x，y)在全平面有连续偏导数，曲线积分
在全平面与路径无关，且
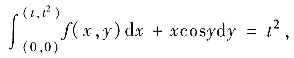
求f(x，y).
答案
参考答案：(Ⅰ)
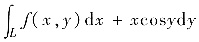在全平面与路径无关
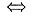
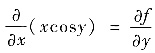，即
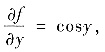
积分得f(x，y)=siny+C(x).
(Ⅱ)求f(x，y)转化为求C(x).
方法1°f(x，y) dx+xcosydy=sinydx+xcosydy+C(x)dx
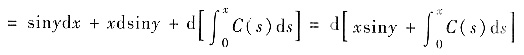
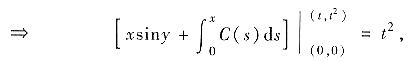
即
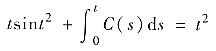
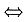sint2+2t2cost2+C(t)=2t.
因此f(x，y)=siny+2x-sinx2-2x2cosx2.
方法2°取特殊路径如图所示，由于
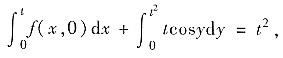
即
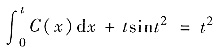
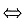C(t)=2t-sint2-2t2cost2.
因此f(x，y)=siny+2x-sinx2-2x2cosx2.
