问题
填空题
设Ω是由曲面x2+y2-z2=0与平面z=2围成的空间区域，则
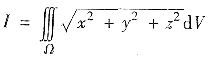的值是______.
答案
参考答案：
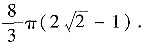
解析：[分析一] 选用球坐标，则Ω的球坐标表示：
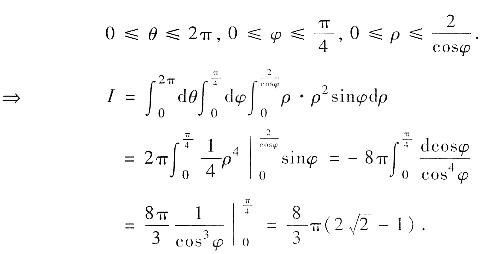
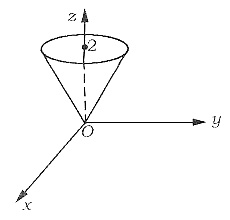
[分析二] 选用柱坐标变换，且选择先对r积分的顺序. 由于
0≤z≤2，D(z)：0≤θ≤2π，0≤r≤z，
搜题请搜索小程序“爱下问搜题”
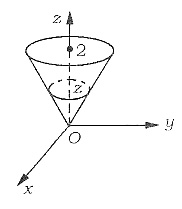
设Ω是由曲面x2+y2-z2=0与平面z=2围成的空间区域，则
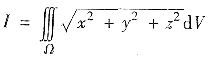的值是______.
参考答案：
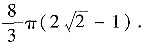
解析：[分析一] 选用球坐标，则Ω的球坐标表示：
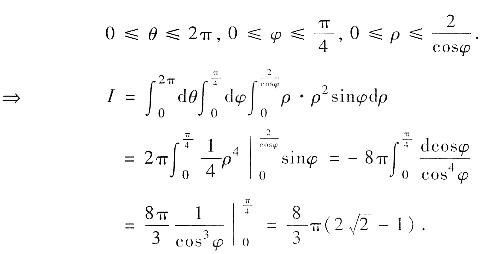
[分析二] 选用柱坐标变换，且选择先对r积分的顺序. 由于
0≤z≤2，D(z)：0≤θ≤2π，0≤r≤z，