参考答案：k(-1，1，1)^T，k≠0为任意常数，

解析：“特征值不同特征向量线性无关”，已知矩阵A只有一个线性无关的特征向量，故特征值λ₀必是3重根，且秩r(λ₀E-A)=2.
由

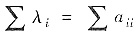知3λ₀=4+(-2)+1，得特征值λ=1(3重). 又

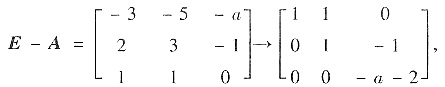
因为秩r(E-A)=2，因此有a=-2. 此时(E-A)x=0的基础解系是(-1，1，1)^T.
故A的特征向量为k(-1，1，1)^T，k≠0为任意常数.
特征值有重根时，要会用秩来分析判断问题.