问题
问答题
已知A=(α1，α2，α3，α4)是4阶矩阵，其中α1，α2，α3，α4是4维列向量. 若齐次方程组Ax=0的通解是k(1，0，-3，2)T，证明α2，α3，α4是齐次方程组A*x=0的基础解系.
答案
参考答案：由解的结构知n-r(A)=1，故秩r(A)=3.
又由
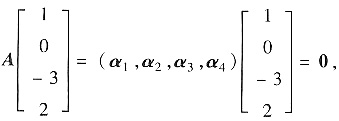得α1-3α3+2α4=0.
因A*A=|A|E=0，即A*(α1，α2，α3，α4)=0，故α2，α3，α4都是A*x=0的解，
由α1=3α3-2α4与r(A)=3有A=(α1，α2，α3，α4)=(3α3-2α4，α2，α3，α4)→0，α2，α3，α4)，可知α2，α3，α4线性无关.
由r(A)=3得r(A*)=1，那么n-r(A*)=3.
综上可知，α2，α3，α4是A*x=0的基础解系.