问题
单项选择题
设
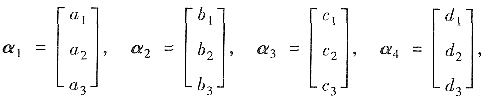则三个平面
a1x+b1y+c1z+d1=0，
a2x+b2y+c2z+d2=0，
a3x+b3y+c3z+d3=0
两两相交成三条平行直线的充分必要条件是
A．秩r(α1，α2，α3)=1，秩r(α1，α2，α3，α4)=2.
B．秩r(α1，α2，α3)=2，秩r(α1，α2，α3，α4)=3.
C．α1，α2，α3中任两个向量均线性无关，且α4不能由α1，α2，α3线性表出.
D．α1，α2，α3中任两个向量均线性无关，且α4可由α1，α2，α3线性表出.
答案
参考答案：C
解析：三个平面两两相交，说明方程组
必无解.
因此r(α1，α2，α3)≠r(α1，α2，α3，α4)，可排除D.
而r(α1，α2，α3)=1，说明三个平面的法向量共线，因此这三个平面必平行或重合，可排除A.
当三个平面两两相交成三条平行直线时，这三个平面的法向量是共面且互不平行的，即(a1，b1，c1)，(a2，b2，c2)，(a3，b3，c3)共面且互不平行，因此
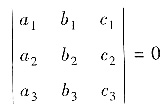且任两行不成比例. 从而秩r(α1，α2，α3)=2. 但当r(α1，α2，α3)=2时，不能保证任意两个平面不平行，故B是必要条件.
由排除法可知，应选C.