问题
填空题
设y(x)是y′″+y′=0的解且x→0时y(x)是x2的等价无穷小,则y(x)=______.
答案
参考答案:2(1-cosx).
解析:令P=y′,则得p″+p=0,它的特征方程是λ2+1=0,于是通解为y′=P=C1cosx+C2sinx,再积分一次,即得原方程的通解是
y=C1sinx-C2cosx+C3.
下面要定出常数C1,C2,C3.
方法1°由泰勒公式
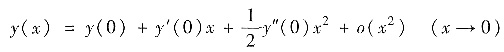
及y(x)~x2(x→0)
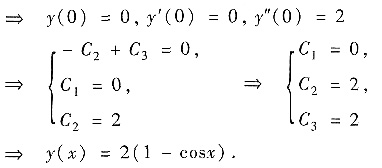
方法2°由

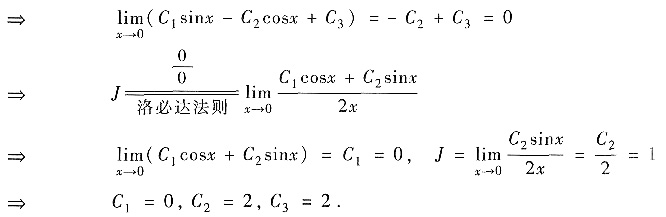
因此y(x)=2(1-cosx)0
