问题
问答题
设x>0时,
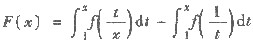 ,其中函数f(x)在区间(0,+∞)上连续且单调增加.试证:F(x)在(0,+∞)也单调增加.
,其中函数f(x)在区间(0,+∞)上连续且单调增加.试证:F(x)在(0,+∞)也单调增加.
答案
参考答案:自然的想法是求F’(x).由于F(x)中的第一项变限积分中被积函数除依赖于积分变量t外,还依赖于x,所以要通过变量替换把积分化为只有积分限含有x的变限积分,然后再求导.于是,令[*],则
[*]
由变限积分求导法得
[*]
为比较上式右端两项的大小,把第一项表成定积分得
[*]
当0<x<1时,由[*]得当[*]时有[*]
当x>1时,由[*]得当[*]时有[*]
代入即得 F’(x)>0(x>0,x≠1),此外还有F’(1)=0.
因此,F(x)在(0,+∞)单调增加.
