问题
问答题
设有抛物线C1:x2=ay和圆C2:x2+y2=2y,
(Ⅰ) 确定a的取值范围,使得C1,C2交于三点O,M,P(如图);
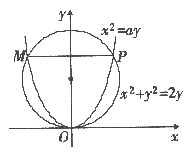
(Ⅱ) 求抛物线C1与弦MP所围平面图形面积S(a)的最大值;
(Ⅲ) 求上述具有最大面积的平面图形绕x轴旋转一周所得旋转体的体积V.
答案
参考答案:(Ⅰ) 方法1° 由[*]得ay+y2=2y,解得y=0,y=2-a.由0<y=2-a<2可得,0<a<2.
方法2° C1,C2交于三点O,M,P的充要条件是a>0,且抛物线C1在原点处的曲率K>1(圆C2的曲率为1).由于[*],所以C1在原点处的曲率为
[*]
因此,当0<a<2时,C1,C2交于三点O,M,P.
[*]
(Ⅱ) 两曲线x2=ay,x2+y2=2y的交点为O(0,0),[*],由定积分的几何意义及对称性可得所论平面图形面积
[*]
要使S(a)最大,只要f(a)=a(2-a)3最大.由于S’(a)=2(2-a)2(1-2a),f"(a)=-4(2-a)(1+a)<0,令f’(a)=0,解得唯一驻点[*],所以点[*]为最大值点,此时,所求面积的最大值为
[*]
(Ⅲ) 由定积分的几何意义可得所求旋转体的体积(圆柱体的体积减去二倍抛物旋转体的体积,如图)为
[*]