问题
问答题
已知矩阵
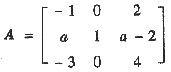 有三个线性无关的特征向量,求a的值,并求An.
有三个线性无关的特征向量,求a的值,并求An.
答案
参考答案:由矩阵A的特征多项式
[*]
知矩阵A的特征值是1,1,2.
因为A有3个线性无关的特征向量,所以秩 r(E-A)=1.又
[*]
故 a=1.
由(E-A)x=0,即[*]
得基础解系 α1=(1,0,1)T,α2=(0,1,0)T.
由 (2E-A)x=0,即[*]
得基础解系 α3=(2,-1,3)T.
那么令P=(α1,α2,α3),有[*]从而 A=PΛP-1.
于是 An=PΛnP-1
[*]
评注 要搞清相似对角化的充分必要条件,掌握相似对角化的应用求An.
