问题
问答题
设f(x)在[0,a]上有一阶连续导数,证明:至少存在一点ξ∈[0,a],使得
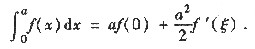
答案
参考答案:[证明一] 利用f(x)=f(0)+f’(ξ1)(x-0)=f(0)+f’(ξ1)x可得因f’(x)在[0,a]上连续,由闭区间上连续函数的最大值最小值定理知,存在m和M,使m≤f’(x)≤M,于是在[0,a]上有mx≤xf’(ξ1)≤Mx,故
[*]
即[*]
由连续函数的介值定理知,至少存在一点ξ∈[0,a],使得[*]即[*],于是
[*]
[证明二] [*]
因为f’(x)连续,x-a≤0(x∈[0,a]),故由积分中值定理知,至少存在一点ξ∈[0,a],使得
[*]
于是[*]
[证明三] 令[*]则F(x)可用麦克劳林公式表示为
[*]
即[*]
令x=a得[*]
解析:
[分析]: 所给问题为f(x)的定积分与f’(ξ)之间的关系.可以考虑成原函数与F"(ξ)之间的关系,从而可利用二阶泰勒公式来证明.
如果认定为考察f(x)与f’(ξ)之间关系,也可以利用拉格朗日中值定理(一阶泰勒公式)来证明.
也可以利用积分中值定理[*]来证明.
