问题
填空题
已知a,b满足
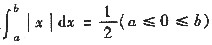 ,则曲线y=x2+ax与直线y=bx所围区域的最大面积与最小面积分别为______.
,则曲线y=x2+ax与直线y=bx所围区域的最大面积与最小面积分别为______.
答案
参考答案:
[*]
解析:
[分析]: 因为
[*]
故常数a与b除满足a≤0≤b外还满足a2+b2=1.又曲线y=x2+ax与直线y=bx交于x=0与x=b-a,从而它们所围图形的面积为
[*]
应用拉格朗日乘数法,令[*],则由
[*]
解得驻点[*]此时[*]又弧a2+b2=1且a≤0≤b的两个端点处a分别为0与-1,当a=0时b=1,此时[*]当a=-1时b=0,此时[*]故所求面积的最大值为[*]最小值为[*]
