问题
解答题
宏志中学九年级300名同学毕业前夕给灾区90名同学捐赠了一批学习用品（书包和文具盒），由于零花钱有限，每6人合买一个书包，每2人合买一个文具盒（每个同学都只参加一件学习用品的购买），书包和文具盒的单价分别是54元和12元。
（1）若有x名同学参加购买书包，试求出购买学习用品的总件数y与x之间的函数关系式（不要求写出自 变量的取值范围）；
（2）若捐赠学习用品总金额超过了2300元，且灾区90名同学每人至少得到了一件学习用品，请问同学们 如何安排购买书包和文具盒的人数？此时选择其中哪种方案，使购买学习用品的总件数最多？
答案
解：（1）若有x名同学参加购买书包，则有（300-x）名同学参加购买文具盒，所以可购买书包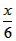
个，购买文具盒
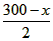个，
所以购买学习用品的总件数y与x之间的函数关系式为：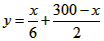
，
即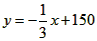
；
（2）设有x名同学参加购买书包，根据题意得
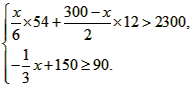
解这个不等式组，得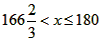
，
又因为6人合买一个书包，故购买书包的人数应为6的倍数，
所以购买书包的人数应为：168或174或180，
相应购买文具盒的人数为：132或126或120，
∵总件数y与x的关系式为：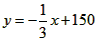
，y随x的增大而减小，
∴当x=168时，购买学习用品的总件数最多。