问题
解答题
某商场经营某种品牌的童装,购进时的单价是60元,根据市场调查,在一段时间内,销售单价是80元时,销售量是200件,而销售单价每降低1元,就可多售出20件。
(1)写出销售量y件与销售单价x元之间的函数关系式;
(2)写出销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式;
(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,则商场销售该品牌童装获得的最大利润是多少?
答案
解:(1)由题意,得:y=200+(80-x)·20=-20x+1800,
∴销售量y件与销售单价x元之间的函数关系式为:y=-20x+1800;
(2) 由题意,得:w=(x-60)(-20x+1800)=-20x2+3000x-108000,
∴利润w元与销售单价x元之间的函数关系式为:w=-20x2+3000x-108000;
(3) 由题意,得: ,解得76≤x≤78,
,解得76≤x≤78,
对于w=-20x2+3000x-108000,对称轴为x=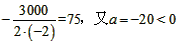 ,
,
∴当76≤x≤78时,w随x增大而减小,
∴当x=76时,wmax=(76-60)(-20×76+1800)=4480,
∴商场销售该品牌童装获得的最大利润是4480元。
