问题
问答题
函数f(x)在[0,+∞)上可导,且f(0)=1,满足等式

证明:当x≥0时,成立不等式e-x≤f(x)≤1
答案
参考答案:由
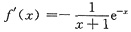 ①
①
且x≥0,
则有不等式
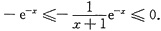
两边积分,利用式①有e-x≤f(x)-f(0)≤0,
即有不等式e-x≤f(x)≤1.
解析: 先在所给等式两边求导得到f(x)的二阶微分方程.为求f’(x),视f’(x)为因变量,化为一阶微分方程而求之.求出f’(x)的表示式后再放缩化为不等式,最后积分即可得到f(x)的不等式.
