问题
问答题
已知an=
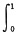x2(1-x)ndx，证明级数
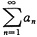收敛，并求这个级数的和．
答案
参考答案：
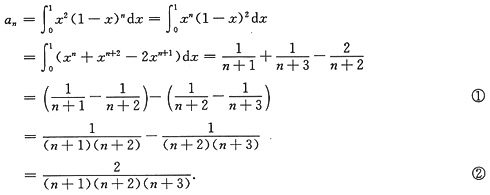
由式②得
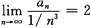．因
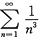收敛，故正项函数
收敛．
又由式②与式①得到
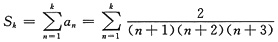
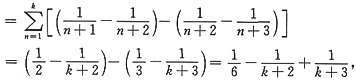
故
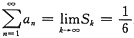．所以该级数收敛，其和为
．
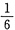解析： 先求出an的分式表示式，再证明其部分和有极限．求出此极限也就求出了该级数的和．其中，可利用公式
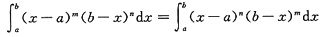简化求出an的分式表示式．
搜题请搜索小程序“爱下问搜题”
已知an=
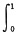x2(1-x)ndx，证明级数
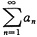收敛，并求这个级数的和．
参考答案：
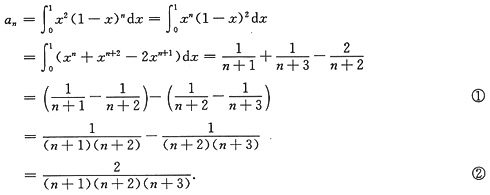
由式②得
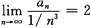．因
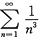收敛，故正项函数
收敛．
又由式②与式①得到
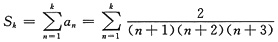
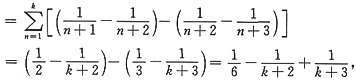
故
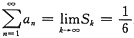．所以该级数收敛，其和为
．
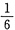解析： 先求出an的分式表示式，再证明其部分和有极限．求出此极限也就求出了该级数的和．其中，可利用公式
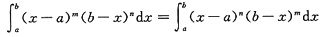简化求出an的分式表示式．
，下列说法错误的是