参考答案：D

解析： 利用泰勒展开式及相关概念的定义判别之．
解一 由泰勒公式及题设得到

故当|x|充分小且x＜0时，f(x)-f(0)＜0；当x＞0时，f(x)-f(0)＞0．因而f(0)不是极值，排除A、B．
又将f"(x)按皮亚诺余项展开，有
f"(x)=f"(0)+f"’(0)x+o(x)=f"’(0)x+o(x)．
当|x|充分小且x＜0时，f"(x)＜0(因f"’(0)＞0)，故曲线y=f(x)在点(0，f(0))的左侧邻域为凸．
当x＞0时，因f"’(0)＞0，故f"(x)＞0，则曲线y=f(x)在点(0，f(0))的右侧邻域为凹．仅D入选．
解二 利用

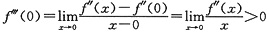可得到上述结论．
事实上，由x＜0得到在点(0，f(0))的左侧邻域f"(x)＜0，曲线y=f(x)为凸；当x＞0时，f"(x)＞0，故在点(0，f(0))的右侧邻域为凹．