参考答案：[解] (Ⅰ) 设通解为y_t=C·2^t+At+B，其中C为任意常数，A与B为待定常数，代入方程得
y_t+1-2y_t=C·2^t+1+A(t+1)+B-2C·2^t-2(At+B)

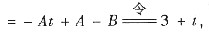
可确定A=-1，B=-4，故方程的通解为y_t=C·2^t-t-4．
(Ⅱ) 设通解为y_t=C+At²+Bt，其中C为任意常数，A与B为待定常数，代入方程得

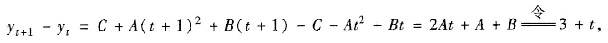
可确定

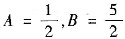，故方程的通解为

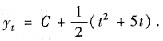
(Ⅲ) 设通解为y_t=C+A·2^t，其中C为任意常数，A为待定常数，代入方程得

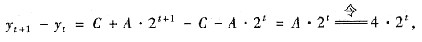
可确定A=4，故方程的通解为y_t=C+4·2^t．
(Ⅳ) 设通解为y_t=C·2^t+At·2^t，其中C为任意常数，A为待定常数，代入方程得
y_t+1-2y_t=C·2^t+1+2A(t+1)·2^t-2C·2^t-2，4t·2^t

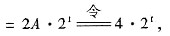
可确定A=2，故方程的通解为y_t=(C+2t)·2^t．