问题
问答题
设f(x)是区间[a,b]上单调减少的连续函数,且f(x)>0在[a,b]上成立.求证:在(a,b)内存在唯一的c,使在区间[a,c]上以y=f(x)为曲边的曲边梯形的面积与在[c,b]上以f(c)为高的矩形面积相等.
答案
参考答案:[分析与证明]
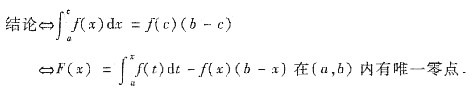
由题设知F(x)在[a,b]上连续,且
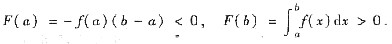
于是,由闭区间上连续函数的性质知,F(x)在(a,b)内必有零点.为证明零点的唯一性,只需证明F(x)在[a,b]上是单调的.设a≤x1<x2≤b,则
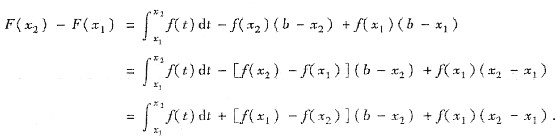
因为上式右端第一项与第三项为正,第二项非负,故F(x)在[a,b]上单调增加,这就证明了c点的唯一性.
