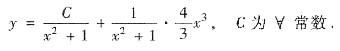(Ⅰ) 已知(x2+2x)y’+y=0,求通解;
(Ⅱ) 已知xy’=y(1+lny-lnx),求通解;
(Ⅲ) 已知
 ,求通解及满足y(0)=1的特解;
,求通解及满足y(0)=1的特解;
(Ⅳ) 求微分方程
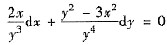 的通解及满足y(1)=1的特解;
的通解及满足y(1)=1的特解;
(Ⅴ) 已知
 分别有解
分别有解
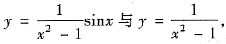 求方程
求方程
 满足y(0)=1的特解;
满足y(0)=1的特解;
(Ⅵ) 已知
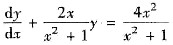 有特解
有特解
 ,求该方程的通解.
,求该方程的通解.
参考答案:[解] 先判断方程的类型,然后再按照方程的类型采用相应的方法求解.
(Ⅰ) 这是可分离变量方程.分离变量得
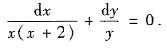
积分得
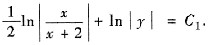
整理即得通解xy2=C(x+2),C为任意常数.
(Ⅱ) 方程可写为
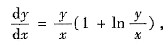
这是齐次方程.于是令
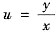 (即y=ux),方程变成关于u与x的可分离变量方程
(即y=ux),方程变成关于u与x的可分离变量方程
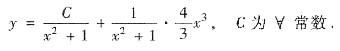
分离变量得
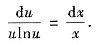
积分得 ln|lnu|=lnx+C1,即 lnu=Cx,解出得u=eCx.
因此原方程通解为 y=xeCx,C为任意常数.
(Ⅲ) 这是一阶线性方程,两边乘
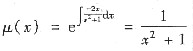 得
得
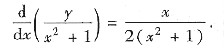
积分得
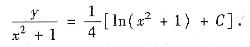
即原方程的通解为
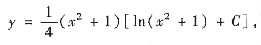
其中C为任意常数.令x=0,由y(0)=1 可得 C=4.
因此,满足y(0)=1的特解为
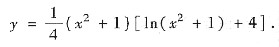
(Ⅳ) 方法1° 两边乘以y4后并改写成
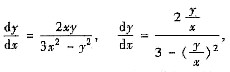
这是齐次方程.令
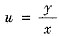 ,原方程变成可分离变量的方程
,原方程变成可分离变量的方程
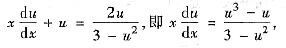
分离变量得
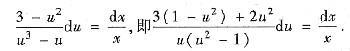
积分得
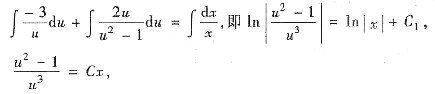
代入
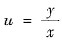 ,得通解
,得通解
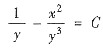 ,其中C为
,其中C为
 常数.
常数.
令x=1,y=1得C=0,于是得满足y(1)=1的特解y=x.
方法2° 易凑微分将方程改写成
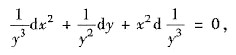
由微分法则得
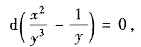
因此,通解为
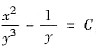 ,其中C为
,其中C为
 常数.
常数.
同前得特解.
(Ⅴ) 由一阶线性方程通解的结构得该一阶线性非齐次方程的通解为
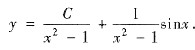
由y(0)=1
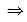 C=-1.因此特解为
C=-1.因此特解为
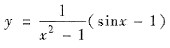 .
.
(Ⅵ) 由一阶线性方程解的叠加原理
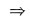
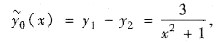
从而
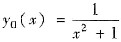 是相应齐次方程
是相应齐次方程
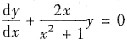 的非零特解.
的非零特解.
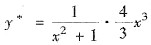 是原非齐次方程的一个特解.因此原方程的通解是
是原非齐次方程的一个特解.因此原方程的通解是