参考答案：[证明] 因ξ∈(0，1)，故

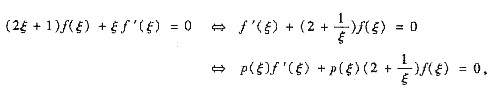
其中

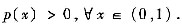
若函数p(x)还满足p’(x)=p(x)(2+

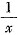)当x∈(0，1)时成立，则要证的结论

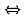[p(x)f(x)]’在(0，1)内有零点．
这启发我们考虑辅助函数F(x)=p(x)f(x)，其中p(x)当x∈(0，1)时满足

可取lnp(x)=2x+lnx， 即 p(x)=xe^2x．
由题设知f(x)=xe^2xf(x)在[0，1]上连续，在(0，1)内可导，且F(0)=0，F(1)=e²f(1)=0，即F(x)在[0，1]上满足罗尔定理的全部条件，故至少存在一点ξ∈(0，1)，使f’(ξ)=(e^2ξf+2ξe^2ξ)f(ξ)+ξe^2ξf’(ξ)=e^2ξ[(2ξ+1)f(ξ)+ξf’(ξ)]=0，从而
(2ξ+1)f(ξ)+ξf’(ξ)=0．